2023. 3. 15. 18:01ㆍComputer Sciences/Problem Solve
https://www.acmicpc.net/problem/11650
11650번: 좌표 정렬하기
첫째 줄에 점의 개수 N (1 ≤ N ≤ 100,000)이 주어진다. 둘째 줄부터 N개의 줄에는 i번점의 위치 xi와 yi가 주어진다. (-100,000 ≤ xi, yi ≤ 100,000) 좌표는 항상 정수이고, 위치가 같은 두 점은 없다.
www.acmicpc.net
문제 설명
N개의 좌푯값이 입력된다. 그 좌푯값을 x 기준으로 오름차순 정렬한다. 만약 x가 같다면, y 기준으로 오름차순 정렬한다.
풀이 방법
Java의 Arrays.sort()를 사용했고 Comparator를 커스텀해서 해결했다.
package baekjoon.sort;
import java.io.*;
import java.util.*;
public class BOJ11650 {
final static int X = 0;
final static int Y = 1;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
int[][] arr = new int[N][2];
for (int i = 0; i < N; i++) {
String[] split = br.readLine().split(" ");
arr[i][X] = Integer.parseInt(split[0]);
arr[i][Y] = Integer.parseInt(split[1]);
}
Arrays.sort(arr, (p1, p2) -> {
return p1[X] != p2[X] ? p1[X] - p2[X] : p1[Y] - p2[Y];
});
StringBuilder sb = new StringBuilder();
for (int[] p : arr) {
sb.append(p[X]).append(" ").append(p[Y]).append("\n");
}
sb.delete(sb.length() - 1, sb.length());
System.out.print(sb);
}
}Arrays.sort()
Java는 기본적으로 배열과 컬렉션에 대한 정렬을 지원해준다. Arrays.sort()가 배열에 대한 정렬을 해주는 메서드이다. 이 메서드는 Tim Sort를 기반으로 동작한다.

정렬 전 LegacyMergeSort.userRequested 라는 값으로 분기를 하는데 이는 자바 환경 변숫값인 -Djava.util.Arrays.useLegacyMergeSort=true 로 설정할 수 있다. 기본적으로는 false가 되며 Tim Sort가 동작한다.
Collections.sort()
이 메서드는 컬렉션에 대해 정렬을 해주는 메서드이다. 다만 파라미터로 리스트를 입력해야 한다.

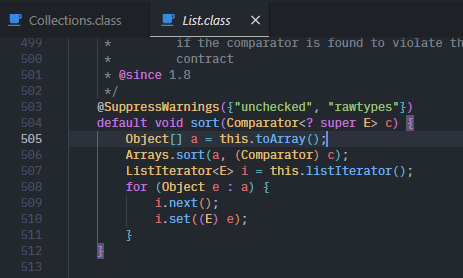
재미있는 점은 내부에서 리스트를 배열로 변환한 뒤 Arrays.sort()를 호출한다는 점이다. 따라서 Collections.sort()도 기본적으로 Tim Sort로 동작한다.
Tim sort
Tim sort는 2002년 Tim Perters가 개발한 정렬 알고리즘이다. 이 알고리즘은 Insertion sort와 Merge sort를 결합하여 만든 실생활 데이터 특성을 고려한 정렬이다. 최선의 시간 복잡도는 O(n), 평균 및 최악의 시간 복잡도는 O(n log n)을 보장하며 기존 Merge sort에 비해 적은 추가 메모리를 사용하여 다른 O(n log n) 정렬 알고리즘의 단점을 최대한 극복한 알고리즘이다. 자세한 설명은 네이버 D2에 작성된 글을 참고하도록 하자.
https://d2.naver.com/helloworld/0315536
'Computer Sciences > Problem Solve' 카테고리의 다른 글
| [Baekjoon] 1967번: 트리의 지름 (0) | 2023.03.16 |
|---|---|
| [Baekjoon] 10814번: 나이순 정렬 (0) | 2023.03.15 |
| [Baekjoon] 2563번: 색종이 (0) | 2023.03.14 |
| [Baekjoon] 25206번: 너의 평점은 (0) | 2023.03.13 |
| [Baekjoon] 10988번: 팰린드롬인지 확인하기 (0) | 2023.03.13 |