2023. 3. 22. 15:25ㆍComputer Sciences/Problem Solve
https://www.acmicpc.net/problem/1074
1074번: Z
한수는 크기가 2N × 2N인 2차원 배열을 Z모양으로 탐색하려고 한다. 예를 들어, 2×2배열을 왼쪽 위칸, 오른쪽 위칸, 왼쪽 아래칸, 오른쪽 아래칸 순서대로 방문하면 Z모양이다. N > 1인 경우, 배열을
www.acmicpc.net
문제 설명
크기가 2^N x 2^N인 2차원 배열을 Z 모양으로 탐색한다. 예를 들어 2x2 배열이면 (0, 0) -> (0, 1) -> (1, 0) -> (1, 1) 순서대로 탐색하면 Z 모양이 된다.
N이 주어졌을 때 r행 c열을 몇 번째로 방문하는지 출력하는 프로그램을 작성해야 한다.
풀이 방법
이 문제는 재귀를 활용하여 해결할 수 있다.
N = 3, r = 6, c = 5 인 경우를 생각해보자.
함수는 solve(int size, int r, int c)로 호출한다. 이때 size는 2^N의 값이므로 8이 되며, r = 6, c = 5이 된다.
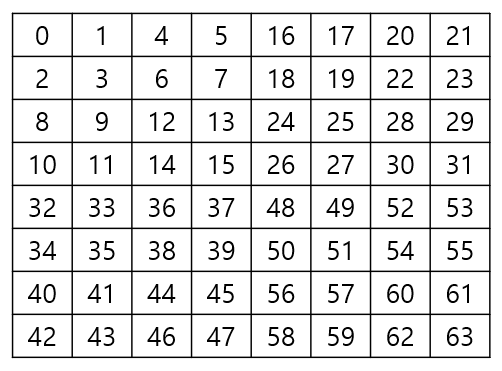
이를 4분면으로 생각해보면 다음과 같다.

노랑색은 1사분면, 주황색은 2사분면, 파란색은 3사분면, 초록색은 4사분면이다(수학의 4사분면과는 다르다).
우리는 (6, 5)가 몇 번째인지를 찾아야 한다. 그렇다면 4사분면으로 탐색 범위를 좁혀야 한다.
이를 위해 먼저 앞선 47까지의 처리를 위해 카운트 값을 처리해줘야 한다. 이는 size * size / 4 * 3 이라는 수식으로 처리할 수 있다. 원리는 다음과 같다.
- 탐색할 위치가 1사분면인 경우 따로 카운팅할 필요가 없다. 현재 탐색할 범위가 1사분면이기 때문이다.
- 탐색할 위치가 2사분면인 경우 size * size / 4 * 1 을 해주어야 한다. 예를 들어 (0, 5) 를 탐색해야 한다고 하면 8x8 배열에서 15까지를 방문한 처리를 해야 하므로 현재 탐색 범위에서 4를 나누어 준다. 즉, 8x8에서 1사분면을 빼는 것이다. 따라서 카운트를 8 * 8 / 4 = 16 을 카운트해서 2사분면으로 탐색할 범위를 정한다.
- 탐색할 위치가 3사분면인 경우 size * size / 4 * 2 를 해주어야 한다. 예를 들어 (5, 0) 를 탐색해야 한다고 하면 8x8 배열에서 31까지를 방문한 처리를 해야 하므로 현재 탐색 범위에서 4를 나누어 준 뒤 2를 곱한다. 즉, 8x8에서 1사분면, 2사분면을 빼는 것이다. 따라서 카운트를 8 * 8 / 4 * 2 = 32 를 카운트해서 3사분면으로 탐색할 범위를 정한다.
- 탐색할 위치가 4사분면인 경우 size * size / 4 * 3 을 해주어야 한다. 예를 들어 (5, 5) 를 탐색해야 한다고 하면 8x8 배열에서 47까지를 방문한 처리를 해야 하므로 현재 탐색 범위에서 4를 나누어 준 뒤 3를 곱한다. 즉, 8x8에서 1, 2, 3사분면을 빼는 것이다. 따라서 카운트를 8 * 8 / 4 * 3 = 48 를 카운트해서 4사분면으로 탐색할 범위를 정한다.
이제 탐색할 범위를 4사분면으로 하기 위해 탐색 범위를 8 -> 4로 줄인다. 또한 그렇게 되면 찾을 r과 c 또한 변화를 주어야 한다. 왜냐하면 탐색 범위의 크기를 8x8 배열에서 4x4 배열로 줄였기 때문이다. 또한 4사분면이기 때문에 상대적인 값으로 r = r - size / 2, c = c - size / 2 라는 처리를 해주어야 한다. 즉 size = 8 / 2 = 4, r = 6 - 8 / 2 = 2, c = 5 - 8 / 2 = 1이 되며 함수 호출은 solve(4, 2, 1) 이 된다.
이제 다음 탐색할 범위를 보면 다음과 같다.
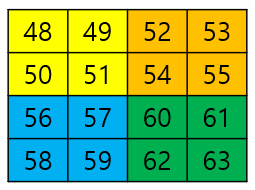
우리가 찾아야 할 값이 (2, 1) 이므로 3사분면으로 범위를 좁히자.
먼저 size를 절반으로 줄인다. 그리고 3사분면까지 방문 카운트를 계산해야 한다. 따라서 count = 48(기존값) + ( size * size / 4 ) * 2 = 48 + ( 4 * 4 / 4 ) * 2 = 48 + 8 = 56 으로 계산할 수 있다. 또한 3사분면에 대한 상대적인 위치값을 계산해야 하므로 r 값을 r - size / 2 처리해서 호출할 때 넘겨준다. 따라서 2x2 배열로 줄게 되며 size = 4 / 2 = 2, r = 2 - 4 / 2 = 0, c = 1 이 되며 함수 호출은 solve(2, 0, 1)가 된다.
다시 3사분면으로 들어가보자.

찾아야 할 값이 (0, 1)이므로 2사분면으로 범위를 좁히자.
먼저 size를 절반으로 줄인다. 그리고 2사분면까지 방문 카운트를 계산한다. 따라서 count = 56 + ( 2 * 2 / 4 ) * 1 = 56 + 1 = 57 로 계산할 수 있다. 또한 2사분면에 대한 상대적인 위치값을 계산해야 하므로 c 값을 c - size / 2 처리해서 호출할 때 넘겨준다. 따라서 1x1 배열로 줄게 되며 size = 2 / 2 = 1, r = 0, c = 1 - 2 / 2 = 0 이므로 함수 호출은 solve(1, 0, 0)이 된다.
다시 2사분면으로 들어가보자.

드디어 원하던 (6, 5) 에 대한 값을 찾았다! 이제 count 값을 출력하기만 하면 된다.
다음은 이를 구현한 코드이다.
import java.io.*;
import java.util.Arrays;
class Main {
static int ans = 0;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int[] info = Arrays.stream(br.readLine().split(" ")).mapToInt(Integer::parseInt).toArray();
int N = info[0];
int r = info[1];
int c = info[2];
int size = (int)(Math.pow(2, N));
solve(size, r, c);
System.out.print(ans);
}
private static void solve(int size, int r, int c) {
if (size == 1) {
return;
}
// 1사분면
if (r < size / 2 && c < size / 2) {
solve(size / 2, r, c);
} // 2사분면
else if (r < size / 2 && c >= size / 2) {
ans += size * size / 4;
solve(size / 2, r, c - size / 2);
} // 3사분면
else if (r >= size / 2 && c < size / 2) {
ans += (size * size / 4) * 2;
solve(size / 2, r - size / 2, c);
} // 4사분면
else {
ans += (size * size / 4) * 3;
solve(size / 2, r - size / 2, c - size / 2);
}
}
}
'Computer Sciences > Problem Solve' 카테고리의 다른 글
| [Baekjoon] 2003번: 수들의 합 2 (0) | 2023.03.24 |
|---|---|
| [Baekjoon] 2023번: 신기한 소수 (0) | 2023.03.23 |
| [Baekjoon] 18870번: 좌표 압축 (0) | 2023.03.21 |
| [Baekjoon] 1389번: 케빈 베이컨의 6단계 법칙 (0) | 2023.03.21 |
| [Baekjoon] 2108번: 통계학 (0) | 2023.03.20 |