2023. 4. 12. 00:02ㆍComputer Sciences/Compiler
1. 오토마타란?
디지털 컴퓨터의 추상적 모델로서 입력 자료를 읽는 입력장치, 출력을 하는 출력장치, 무한개의 기억 소자로 이루어진 임시 기억장치, 유한개의 내부 상태 중 하나의 상태를 항상 유지하는 제어장치로 구성된다. 글로 써놓으니 와닿지는 않는데 그냥 컴퓨터를 추상적으로 표현한 것과 같다. 오토마타는 결정적 오토마타와 비결정적 오토마타로 구분할 수 있다.
결정적 오토마타(deterministic automata)
- 한 상태에서 하나의 입력을 받았을 때 다음 상태가 유일하다.
비결정적 오토마타(non-deterministic automata)
- 한 상태에서 하나의 입력을 받았을 때 다음 상태가 두 개 이상인 것을 말한다.
지금은 무슨 뜻인지 몰라도 된다. 뒤에서 다시 나오니 이런 것이 있다 정도만 알고 넘어가자.
오토마타도 여러 종류가 있는데 이 중 가장 간단한 형태인 유한 오토마타를 알아보자.
2. 유한 오토마타
유한 오토마타는 형식 언어, 즉 알파벳 \(\sum \)로부터 만들어지는 문자열의 부분집합을 인식하는 시스템의 수학적 모델로, 그 시스템에서 변화할 수 있는 상태가 유한개인 것을 말한다. 유한 오토마타는 컴퓨터의 여러 분야에서 널리 사용되고 있으며, 특히 플립플롭(filp-flop)을 비롯한 컴파일러의 어휘 분석기 등에 사용된다.
유한 오토마타를 표현하는 방법은 상태 전이도와 같은 비형식적 표현 방법과 형식적 표현 방법이 있다.
- 상태 전이도 - 유한 오토마타를 유향 그래프로 나타내는 것이다. 따라서 개념을 쉽게 이해할 수 있기 때문에 일반적으로 유한 오토마타를 설명할 때 많이 사용된다.
- 형식적 표현 - 다섯 가지 구성 요소인 5-tuple로 표현하는 방법이다.
비형식적 표현 방법
유한 오토마타의 각 상태를 노드로 표현하고, 간선은 전이를 나타낸다. 또한 최종 상태는 노드를 이중 원으로 나타내고 시작 상태는 시작 간선으로 표시하는 유향 그래프이다. 전이 함수 \(\delta \)(q, a)=p는 상태 q에서 입력 a를 받아 상태 p로 전이할 때 노드 q에서 노드 p로 가는 라벨이 a인 간선으로 나타낸다. 말로 설명하면 이해하기 어려우니 간단한 예제로 살펴보자. 다음은 정규 표현 (a + b)*abb를 인식하는 유한 오토마타를 상태 전이도로 표현한 것이다.
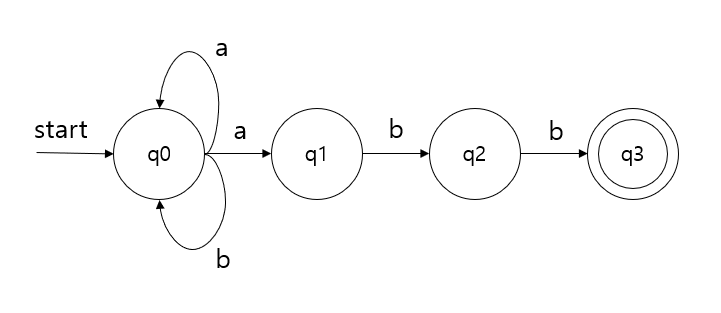
시작 상태 q0에서 b를 입력받으면 q0 상태를 유지하며, a를 입력받으면 q0 상태를 유지하거나 q1 상태로 전이한다. q1 상태에서 b를 입력받으면 q2 상태로 전이하며 q2 상태에서 b를 입력받으면 q3 상태로 전이한다. q3 상태는 최종 상태가 된다. 다른 예 하나만 더 살펴보자. 이번에는 (a + b)abb를 인식하는 유한 오토마타를 상태 전이도로 표현해보자.

형식적 표현 방법
유한 오토마타를 \(M\)이라고 하면
- \(M = (Q, \sum , \delta , q_0, F)\)
- \(Q\) : 상태의 유한 집합
- \(\sum\) : 입력 기호의 유한 집합
- \(\delta\) : 전이 함수로 \(Q \times \sum \to 2^Q\)(\(Q\)의 멱집합)이다. 즉 \(\delta (q, a) = \{ p_1, p_2, \cdots , p_n\}\), 단, \(\{p_1, p_2, \cdots , p_n\} \subseteq Q\)이다.
- \(q_0\) : 시작 상태로 \(q_0 \in Q\)
- \(F\) : 최종 상태로 유한 집합 \(F \subseteq Q\)
보면 알다시피 집합에 대한 개념이 많이 나온다. 전이 함수는 상태의 유한 집합 Q와 입력 기호의 유한 집합 \(\sum\)의 카디션 곱이다. 즉 가능한 모든 상태로 갈 수 있는 경우를 가지므로 Q의 멱집합만큼 개수를 가진다. 단, Q 자기 자신은 제외한 진부분집합이다.
위에서 살펴봤던 정규 표현 (a + b)*abb를 인식하는 유한 오토마타를 형식적으로 표현하면 다음과 같다.
- \(M = (Q, \sum , \delta , q_0, F)\)
- \(Q = \{q_0, q_1, q_2, q_3\}\)
- \(\sum = \{a, b\}\)
- \(\begin{align}\delta : \delta (q_0, a) = \{q_0,q_1\} \\ \delta (q_0, b) = \{q_0\} \\ \delta (q_1, b) = \{q_2\} \\ \delta (q_2, b) = \{q_3\}\end{align}\)
- \(q_0 = q_0\)
- \(F = \{q_3\}\)
⚠️티스토리에서 라텍스 문법을 쓰기 너무 힘들어서 다음부터는 손글씨로 대신하겠습니다.
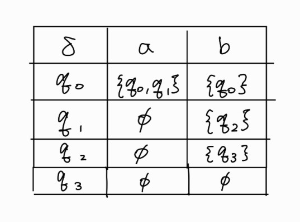
지금처럼 \(Q\)와 \(\sum \)의 원소가 적을 때는 상관없지만 많아진다면 이에 대한 전이 함수를 모두 작성하기에는 무리가 있다. 이를 상태 전이표를 통해 만들 수 있다. 위의 경우 다음과 같이 만들 수 있다.
만약 전이 함수가 상태와 입력에 해당하는 위치에 값이 없다면 상태 전이표에서 그 위치에 \(\varnothing\)을 넣어준다.
결정적 오토마타 vs 비결정적 오토마타
앞에서 언급했듯이 오토마타는 결정적 오토마타와 비결정적 오토마타로 구분된다. 결정적 오토마타는 한 상태에서 오직 하나의 다음 상태로의 이동이 결정되지만, 비결정적 오토마타는 한 상태에서 여러 개의 다음 상태로의 이동이 가능하다.
유한 오토마타도 결정적 유한 오토마타(deterministic finite automata, DFA)와 비결정적 유한 오토마타(nondeterministic finite automata, NFA)로 구분된다. 이는 전이 함수 \(Q \times \sum \to 2^Q\)에 따라 구분하는데, \(2^Q\)가 하나의 상태이면 DFA, \(2^Q\)가 2개 이상의 상태를 나타내면 NFA라고 한다. 위 예제의 경우 전이 함수 중 \(\delta (q_0, a)=\{q_0, q_1\}\) 이므로 NFA이다. 이제 각 오토마타를 확인하고 인식해보자.
3. 결정적 유한 오토마타(DFA)
DFA는 다음과 같은 두 가지 조건을 만족해야 한다.
- \(\varepsilon\)에 의한 상태 전이가 없다.
- \(\delta (q, a)=\{p_1, p_2, \cdots , p_n\}\)에서 n = 1이다. 즉, \(\delta : Q \times \sum \to Q\)
다시 말해 임의의 상태에서 하나의 입력 기호에 대해 다음 상태가 단 하나이거나 상태 전이가 없어야 한다.
💡\(\varepsilon\)에 의한 상태 전이를 \(\varepsilon\)-전이라고도 한다.
이제 DFA를 확인하는 연습을 해보자. 위에서 봤던 (a + b)abb가 DFA인지 확인해보자. 상태 전이도를 다시 보자.

이를 형식적으로 표현하면 다음과 같다.
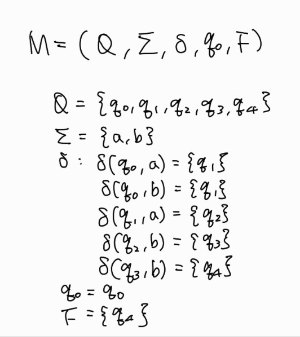
\(\varepsilon\)-전이가 없고, 임의의 상태에서 하나의 입력에 대해 다음 상태가 하나뿐이므로 DFA이다.
한 번 더 연습해보자. 이번에는 0과 1이 짝수 개인 문자열을 받아들이는 유한 오토마타가 DFA인지 알아보고 상태 전이도로 표현해보자.
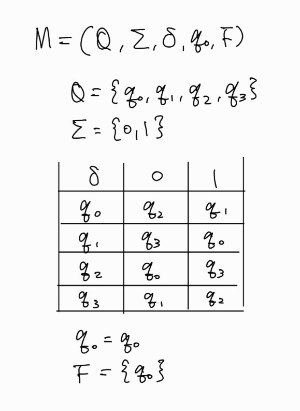
이 또한 \(\varepsilon\)-전이가 없고, 임의의 상태에서 하나의 입력에 대해 다음 상태가 하나 뿐이므로 DFA이다. 이를 상태 전이도로 표현하면 다음과 같다.

이제 DFA에 의해 문장이 인식되는 과정을 살펴보자.
위 오토마타를 활용해서 0101을 인식하는 과정을 살펴보자.
시작 상태가 q0이므로 다음과 같은 과정을 거친다.
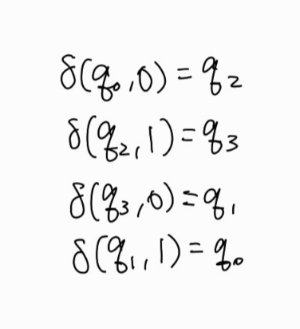
모든 입력을 읽은 후 마지막에 도달한 상태가 q0이며, 최종 상태가 q0이므로 0101은 주어진 DFA에 의해 인식된다고 할 수 있다.
하지만 위 과정에서 한 가지 문제가 있다. 바로 주어진 DFA에 의해 인식되는 문자열이 무엇인지 알기 어렵다는 것이다. 다시 말하면 입력 문자열인 0101을 위 과정에서 알기 어렵다는 것이다. 이를 위해 전이 함수를 확장할 수 있다.
- \(\delta : Q \times \sum \to Q \Rightarrow \delta^* : Q \times \sum^* \to Q\)
확장된 전이 함수는 하나의 입력 기호를 문자열로 확장하는 것이다. 즉 다음과 같이 확장해야 한다.
- \(\delta^* (q_0, \varepsilon )=q_0\)
- \(\delta^* (q_0, wa) = \delta (\delta^*(q_0, w), a)\)
여기서 \(w \in \sum^*, a \in \sum \)이다. 즉 q0 상태에서 문자열 wa를 본다는 것은 문자열 w를 모두 본 상태에서 a를 보는 것과 같다는 말이다. 확장된 함수로 바로 위의 오토마타가 0101을 인식하는 것을 다시 확인해보자.
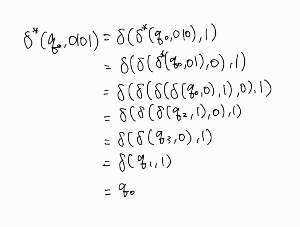
\(q_0 \in F\)이므로 0101은 위 DFA를 통해 인식된다고 할 수 있다.
이제 NFA을 알아보도록 하자.
4. 비결정적 유한 오토마타(NFA)
NFA는 다음과 같은 두 가지 조건을 만족해야 한다.
- \(\varepsilon\)에 의한 상태 전이가 있다.
- \(\delta (q, a)=\{p_1, p_2, \cdots , p_n\}\)에서 n \(\ge\) 2인 n이 하나라도 존재한다. 즉, \(\delta : Q \times \sum \to 2^Q\)
다시 말해 어떤 상태에서 하나의 입력 기호에 대해 다음 상태가 2개 이상인 것이 하나라도 존재한다.
맨 처음에 봤었던 (a + b)*abb의 상태 전이표를 다시 보자.

이 경우 \(\delta (q_0, a) = \{q_0, q_1\}\)이므로 다음 상태가 2개 이상인 것이 존재한다. 따라서 이 유한 오토마타는 NFA이다.
이제 NFA로부터 문장을 인식해보자.
인식하는 과정은 두 가지 방법으로 풀어낼 수 있다. 첫 번째는 전이 함수를 하나하나 모두 적용시켜서 인식하는 방법이고, 두 번째는 갈 수 있는 상태를 그림으로 표현하여 인식하는 방법이다. 그림으로 표현하는 것이 직관적이므로 그림으로 표현하겠다. 위 NFA를 이용해 baabb를 인식해보자.

하지만 이 역시 DFA와 마찬가지로 NFA에 의해 인식되는 문자열이 무엇인지 명확하게 알지 못한다. 즉 baabb라는 문자열이 입력이라는 것을 위 그림만으로 알기 어렵다. 이를 알기 위해 다음과 같이 전이 함수를 하나의 입력 기호에서 입력 문자열로 확장한다.
- \(\delta : Q \times \sum \to 2^Q \Rightarrow \delta^* : Q \times \sum^* \to 2^Q\)
단, \(\delta^*(q, \varepsilon ) = \{q\}\)
\(\delta^*(q, wa)=\{\gamma | \delta^*(q, w)에 의해 도달할 수 있는 모든 상태 p에 대해 \gamma \in \delta (p,a)\} \\ = \bigcup_{p \in \delta^*(q, w)}\delta (p,a)\)
여기서 \(w \in \sum^*, a \in \sum \)이다. 즉 q 상태에서 문자열 wa를 본다는 것은 문자열 w를 모두 본 상태에서 a를 본 상태 집합의 합집합과 같다는 말이다. 이 확장 함수를 baabb에 적용해보자.

\(\{q_0, q_3\} \cap F = \{q_3\}\) 이므로 baabb는 이 NFA에 의해 인식된다고 할 수 있다.
DFA vs NFA
- NFA는 언어의 구조를 간단하고 쉽게 표현할 수 있지만 DFA보다 프로그램으로 구현하기 까다롭다.
- DFA는 프로그램으로 구현했을 때 효율 면에서 NFA보다 훨씬 좋다.
따라서 일반적인 오토마타 구현은 DFA로 하는 것이 매우 효율적이지만 NFA가 언어의 구조를 간단하고 쉽게 표현할 수 있기 때문에 서로 변환이 필요하다. 변환에 대해서는 다음 포스트에서 다루도록 하겠다.
'Computer Sciences > Compiler' 카테고리의 다른 글
| [Compiler] 4-3. NFA -> DFA 변환(2) (0) | 2023.04.13 |
|---|---|
| [Compiler] 4-2. NFA -> DFA 변환(1) (0) | 2023.04.12 |
| [Compiler] 3-3. 문법 표기법 (0) | 2023.04.10 |
| [Compiler] 3-2. 형식 문법 (0) | 2023.04.10 |
| [Compiler] 3-1. 형식 언어 (0) | 2023.03.23 |