2023. 4. 13. 00:07ㆍComputer Sciences/Compiler
이번엔 \(\varepsilon\)-전이가 없는 NFA를 DFA로 변환해보자. 변환 알고리즘은 다음과 같다.
- NFA에 의해 인식되는 언어를 L이라고 하면 L을 인식하는 DFA가 존재한다. L을 인식하는 NFA \(M = (Q, \sum , \delta , q_0, F\)라 하면 L을 인식하는 DFA \(M^\prime = (Q^\prime, \sum , \delta^\prime, q_0^\prime, F^\prime\)는 다음과 같이 구성된다.
- \(Q^\prime = 2^Q\), 즉 \(Q^\prime\)의 한 상태는 \([q_1, q_2, \cdots , q_i]\)의 형태로 나타낸다. 단, \(q_j \in Q(j=1, 2, \cdots , i\)이다.
- \(F^\prime=\{q \in Q^\prime\) | q는 M의 최종 상태를 포함하는 \(Q^\prime\) 안에 있는 모든 상태들의 집합}
- \(q_0^\prime = [q_0]\)
- \(\delta (\{q_1, q_2, \cdots , q_i\}, a) = \{p_1, p_2, \cdots , p_j\}\)라 하면 \(\delta^\prime ([q_1, q_2, \cdots , q_i], a = [p_1, p_2, \cdots , p_j]\)이다.
이는 입력 문자열의 길이에 대해 수학적 귀납법으로 증명하면 되지만 증명은 생략한다.
다음과 같이 \(\varepsilon\)-전이가 없는 NFA에 알고리즘을 적용해서 DFA로 변환해보자.
NFA M = (\(\{q_0, q_1\}, \{0, 1\}, \delta , q_0, \{q_1\}\))
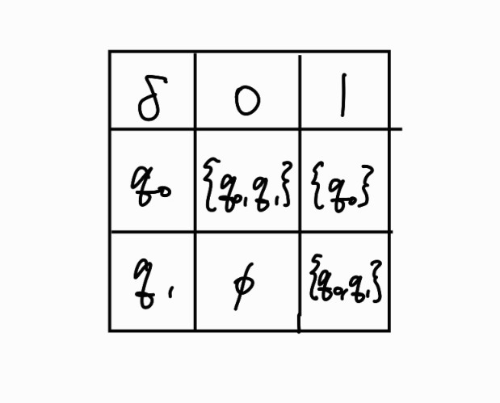
이를 상태 전이도로 나타내면 다음과 같다.
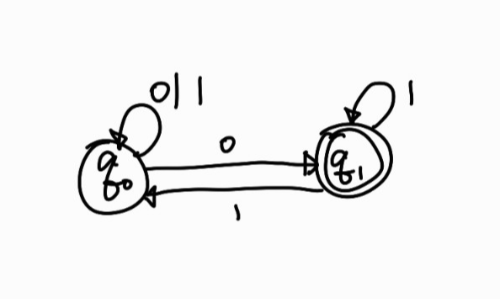
이때 NFA를 DFA로 변환해보자. DFA \(M^\prime = (Q^\prime, \sum , \delta ^\prime, q_0^\prime, F^\prime)\)라 하면 변환 알고리즘에 의해 다음과 같이 된다.
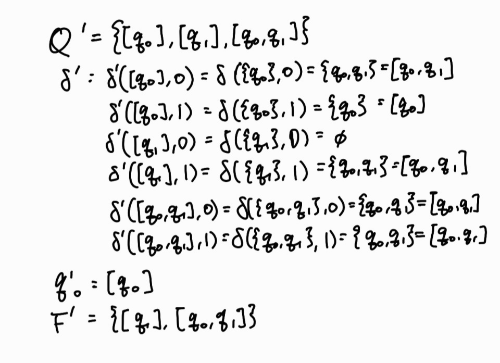
이 전이 함수를 상태 전이표로 나타내면 다음과 같다.

여기서 [q0], [q1], [q0, q1]을 각각 A, B, C라고 하고 상태 전이도를 그리면 다음과 같다.
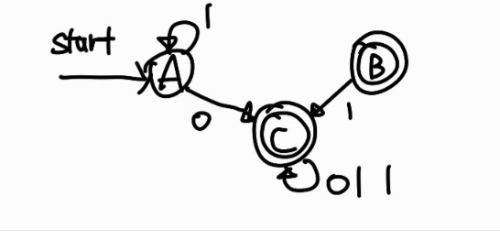
이 상태 전이도는 DFA로 바뀌어져 있지만 B 상태는 시작 상태로부터 도달 불가능한 상태이므로 문장을 인식하는데 불필요하다. 따라서 B 상태를 제거하고 다음과 같은 상태 전이도를 얻을 수 있다.
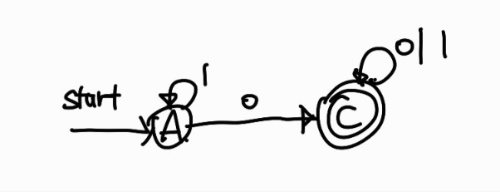
\(\varepsilon\)-전이를 생각하지 않아도 되기 때문에 \(\varepsilon\)-전이가 있는 NFA를 DFA로 변환하는 것보다 과정이 간단하다. 다음엔 \(\varepsilon\)-전이가 없는 NFA를 \(\varepsilon\)-closure를 이용하여 DFA로 변환해볼 것이다.
'Computer Sciences > Compiler' 카테고리의 다른 글
| [Compiler] 4-2. NFA -> DFA 변환(1) (0) | 2023.04.12 |
|---|---|
| [Compiler] 4-1. 유한 오토마타 (0) | 2023.04.12 |
| [Compiler] 3-3. 문법 표기법 (0) | 2023.04.10 |
| [Compiler] 3-2. 형식 문법 (0) | 2023.04.10 |
| [Compiler] 3-1. 형식 언어 (0) | 2023.03.23 |