2023. 4. 12. 21:31ㆍComputer Sciences/Compiler
NFA에서 DFA로 변환하기 전에 NFA와 DFA가 서로 동등해야만 변환의 의미가 있다. 다만 증명 부분은 생략한다. NFA와 DFA는 동등하다는 것만 알고 넘어가자.
\(\varepsilon\)-전이가 있는 NFA를 DFA로 변환
\(\varepsilon\)-closure를 이용하여 변환하는데 NFA에서 의미가 같은 여러 개의 상태가 DFA에서 하나의 상태로 변환되는 것이다. 먼저 \(\varepsilon\)-closure(S)에 대한 정의부터 살펴보자.
\(\varepsilon\)-closure(S)
- S가 하나의 상태일 경우 \(\varepsilon\)-closure(S)는 NFA의 상태 S와 상태 S로부터 \(\varepsilon\)-전이에 의해 도달될 수 있는 NFA의 모든 상태의 결합이다. 이 방법은 \(\varepsilon\)-closure(S)의 원소가 변하지 않을 때까지 반복한다.
- T가 하나 이상의 상태 집합으로 되어 있는 경우 \(\varepsilon\)-closure(T)는 NFA의 상태 T 안에 있는 각각의 상태에 대해 1번 과정과 같은 방법으로 상태들의 집합을 구하여 합집합을 한 것이다.
즉 \(\varepsilon\)-closure(T) = \(\bigcup _{x \in T} \varepsilon\)-closure(x)
\(\varepsilon\)-closure 계산하기
정규 표현 (a + b)*abb를 인식하는 NFA를 상태 전이도로 나타내면 다음과 같다. 이 상태 전이도로부터 \(\varepsilon\)-closure를 구해보자.
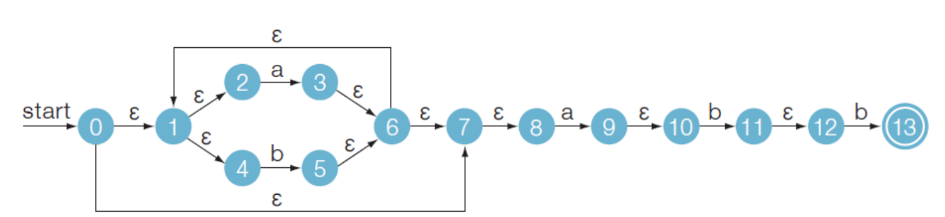
- \(\varepsilon\)-closure(0) = {0, 1, 2, 4, 7, 8}
- 0이라는 상태와 같은 상태를 유지할 수 있는 \(\varepsilon\)-전이를 하면 1, 2가 같은 상태이며 3은 a라는 상태가 되기 때문에 안 된다. 또한 1, 4가 같은 상태이며 5는 b라는 상태이기 때문이 안 된다. 이런 식으로 원래 상태와 같은 상태가 유지되도록 하는 \(\varepsilon\)-전이를 계속 해나가면 된다. 이때 자기 자신은 항상 포함된다.
- \(\varepsilon\)-closure(1) = {1, 2, 4}
- \(\varepsilon\)-closure(2) = {2}
- \(\varepsilon\)-closure(3) = {3, 6, 7, 8, 1, 2, 4}
- \(\varepsilon\)-closure(4) = {4}
- \(\varepsilon\)-closure(5) = {5, 6, 7, 8, 1, 2, 4}
- \(\varepsilon\)-closure(6) = {6, 1, 2, 4, 7, 8}
- \(\varepsilon\)-closure(7) = {7, 8}
- \(\varepsilon\)-closure(8) = {8}
- \(\varepsilon\)-closure(9) = {9, 10}
- \(\varepsilon\)-closure(10) = {10}
- \(\varepsilon\)-closure(11) = {11, 12}
- \(\varepsilon\)-closure(12) = {12}
- \(\varepsilon\)-closure(13) = {13}
이제 NFA를 DFA로 변환해보자. \(\varepsilon\)-closure를 이용하여 \(\varepsilon\)-전이가 있는 NFA를 DFA로 변환하는 방법은 다음과 같다.
- 입력 - \(\varepsilon\)-전이가 있는 NFA
- 출력 - \(\varepsilon\)-전이가 있는 NFA와 동등한 DFA
- 방법
- \(\varepsilon\)-전이가 있는 NFA의 시작 상태 q0에 대해 \(\varepsilon\)-closure(q0)을 구하고 \(\varepsilon\)-closure(q0)을 DFA의 시작 상태로 놓는다.
- DFA의 시작 상태를 집합 Ds에 넣는다.
- 집합 Ds에서 하나의 상태를 꺼낸 다음, 그 상태의 모든 입력 기호에 대해 각각 도달할 수 있는 모든 상태 집합을 구한다. 이를 T1, T2, ... 라 한다. 그런 다음 \(\varepsilon\)-closure(T1), \(\varepsilon\)-closure(T2), ...를 구하여 DFA의 새로운 상태를 만든다. 만약 새로운 상태가 이미 만들어진 상태와 같은 집합이면 DFA의 새로운 상태를 만들지 않고 현재 상태로부터 이전에 만들어진 상태로 입력 기호에 따른 간선만 만든다. 만약 이미 만들어진 상태가 아니라면 새로운 상태로 만들어 집합 Ds에 추가한다. 이미 모든 입력에 대해 적용한 상태는 집합 Ds에서 제거한다.
- 집합 Ds가 공집합이 될 때까지 3번 과정을 반복한다.
- 만들어진 상태 중에서 \(\varepsilon\)-전이가 있는 NFA의 최종 상태를 포함하는 DFA의 상태는 모두 DFA의 최종 상태가 된다.
좀 복잡해 보인다. 예제를 통해 이해해보자. 위 예제에 알고리즘을 적용해서 \(\varepsilon\)-전이가 있는 NFA를 DFA로 변환해보자.
\(\varepsilon\)-전이가 있는 NFA의 시작 상태가 0이 \(\varepsilon\)-closure(0)이 DFA의 시작 상태가 된다. 위에서 구한 것처럼 \(\varepsilon\)-closure(0) = {0, 1, 2, 4, 7, 8} = A라고 하면 Ds = {A}가 된다. DFA의 시작 상태는 다음과 같다.
Ds에서 상태를 꺼낸다. A가 들어있으므로 A를 꺼낸 다음 모든 입력 기호에 대해 각각 도달할 수 있는 모든 상태 집합을 구한다. A = {0, 1, 2, 4, 7, 8} 이다. 하나씩 해보면 결국 도달할 수 있는 상태는 \(\varepsilon\)을 제외하면 a와 b이다. a에 도달한 상태는 3과 9이고, b에 도달한 상태는 5이다. 이는 다음과 같이 표현할 수 있다.
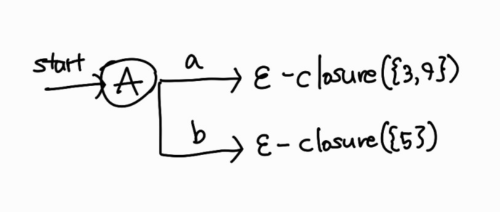
\(\varepsilon\)-closure(3)과 \(\varepsilon\)-closure(9)는 위에서 구해놨다.
- \(\varepsilon\)-closure(3) = {3, 6, 7, 8, 1, 2, 4}
- \(\varepsilon\)-closure(9) = {9, 10}
이 두 집합을 합집합하면 \(\varepsilon\)-closure({3, 9}) = {3, 6, 7, 8, 1, 2, 4, 9, 10} 가 된다. 이를 B라고 하겠다.
그리고 \(\varepsilon\)-closure(5) = {5, 6, 7, 8, 1, 2, 4} = C라고 하고 상태 전이도로 그리면 다음과 같아진다.
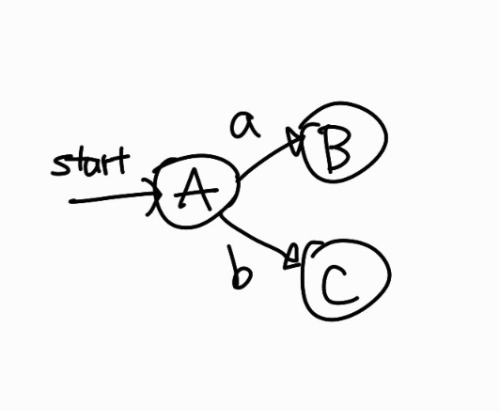
그리고 각 상태를 Ds에 넣어야 한다. 3번을 수행했으므로 A는 꺼낸다. 그럼 Ds = {B, C}가 된다.
Ds가 공집합이 아니므로 Ds에 상태를 꺼내고 과정을 반복한다. B를 꺼내자.
B = {3, 6, 7, 8, 1, 2, 4, 9, 10} 이고 이 상태들에서 도달할 수 있는 상태로는 a와 b가 있으며 a에 도달하는 상태는 {3, 9}이고, b에 도달하는 상태는 {5, 11}이다. 중복 경로를 제외하고 a에 도달하는 경우는 6 -> 1 -> 2 -> 3, 6 -> 7 -> 8 -> 9 가 있고, b에 도달하는 경우는 6 -> 1 -> 4 -> 5, 10 -> 11이 있으므로 위와 같이 도달할 수 있다. 따라서 다음과 같이 그릴 수 있다.
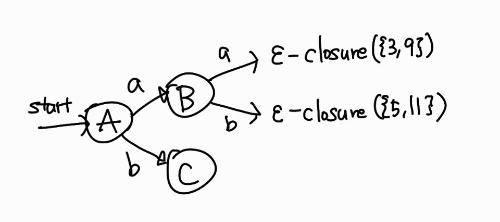
그런데 \(\varepsilon\)-closure({3, 9}) = B와 같으므로 새로운 상태를 생성하지 않고 B를 가리키는 간선만 추가하면 된다. 그리고 \(\varepsilon\)-closure({5, 11}) = D로 두고 그리면 다음과 같이 그릴 수 있다.
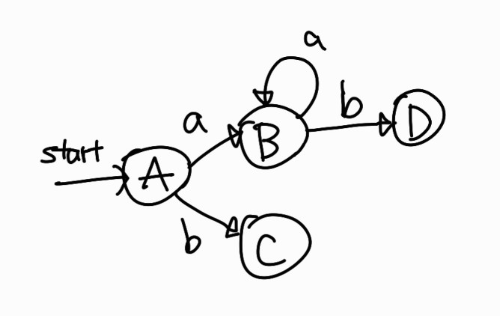
이제 Ds에서 B를 빼고 D를 넣으면 현재 Ds = {C, D}가 된다. 이제 C를 꺼내서 위 과정을 다시 거치자.
C = {5, 6, 7, 8, 1, 2, 4}이고 a와 b에 도달할 수 있는 상태는 a = {3, 9}, b = {5}이다. 따라서 다음과 같이 표현할 수 있다.
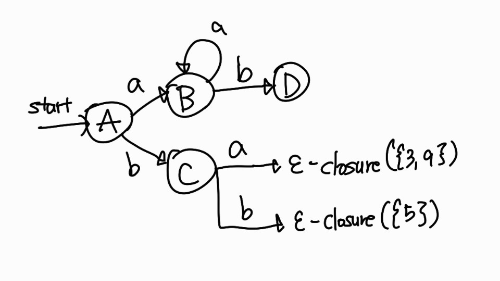
그런데 잘 보니 \(\varepsilon\)-closure({3, 9}) = B이고 \(\varepsilon\)-closure(5) = C 자기 자신이다. 따라서 새로운 상태를 그리지 않고 기존 상태에 간선만 그려서 표현할 수 있다. 이는 다음과 같다.
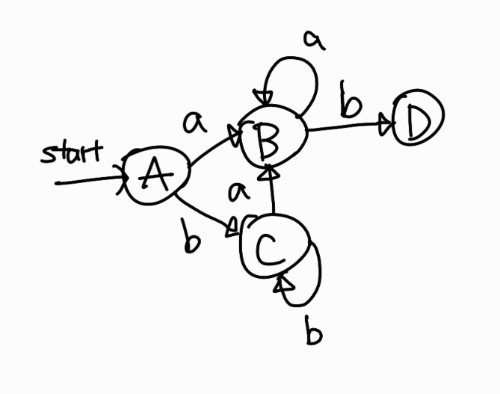
이제 C도 Ds에서 빠지므로 Ds = {D}가 된다. D를 꺼내서 과정을 다시 반복해보자.
D = \(\varepsilon\)-closure({5, 11})이다. 각각을 다시 보면 다음과 같다.
- \(\varepsilon\)-closure(5) = {5, 6, 7, 8, 1, 2, 4}
- \(\varepsilon\)-closure(11) = {11, 12}
이 두 집합의 합집합으로 a와 b에 도달할 수 있는 상태를 구해보자. 그럼 a = {3, 9}, b = {5, 13}이다. 주의할 점은 상태 11은 b라는 상태가 아니라는 것이다. 상태 10에서 b라는 입력이 있어야 상태 11이 b가 되는 것이다.
\(\varepsilon\)-closure({3, 9}) = B이므로 간선을 B를 향해 그리고 \(\varepsilon\)-closure({5, 13}) = E로 두고 표현하면 다음과 같다.
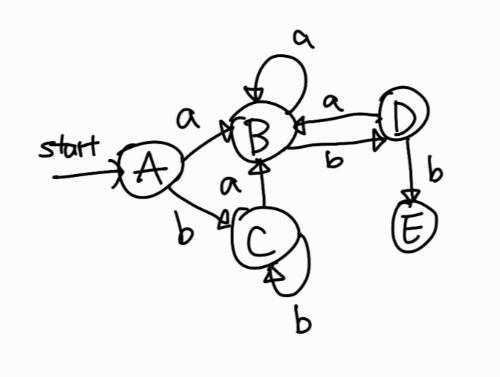
Ds에서 D를 꺼내고 E를 넣으면 현재 Ds는 Ds = {E}가 된다. Ds가 공집합이 아니므로 E를 꺼내서 다시 반복한다.
E = \(\varepsilon\)-closure({5, 13}) = {5, 6, 7, 8, 1, 2, 4, 13}이고 a와 b에 도달하는 상태를 보면 a = {3, 9}, b = {5} 이다. \(\varepsilon\)-closure({3, 9}) = B이므로 간선을 B를 향해 그리면 된다. 그리고 \(\varepsilon\)-closure(5) = C이므로 C를 향하는 간선을 그리면 된다. 따라서 다음과 같이 표현할 수 있다.
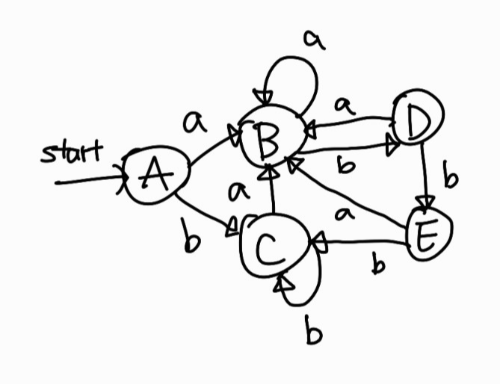
이제 E를 꺼내면 Ds는 공집합이 되므로 반복을 종료한다.
\(\varepsilon\)-전이가 있는 NFA의 최종 상태 13을 포함하는 DFA의 상태를 구하면 E이며, E는 DFA의 최종 상태가 된다. 즉 다음과 같은 상태 전이도와 상태 전이표로 그릴 수 있다.
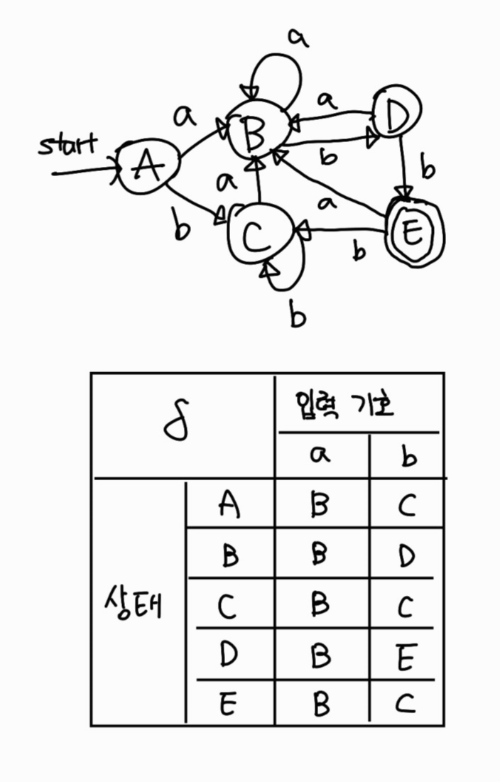
여기서 A가 시작 상태이고 E가 최종 상태이다. 변환된 상태 전이도를 보면 DFA를 만족하므로 \(\varepsilon\)-전이가 있는 NFA를 DFA로 변환에 성공했다.
이번 글에서는 \(\varepsilon\)-전이가 있는 NFA를 DFA로 변환하는 방법을 알아보았다. 다음 글에서는 \(\varepsilon\)-전이가 없는 NFA를 DFA로 변환을 알아보도록 하겠다.
'Computer Sciences > Compiler' 카테고리의 다른 글
| [Compiler] 4-3. NFA -> DFA 변환(2) (0) | 2023.04.13 |
|---|---|
| [Compiler] 4-1. 유한 오토마타 (0) | 2023.04.12 |
| [Compiler] 3-3. 문법 표기법 (0) | 2023.04.10 |
| [Compiler] 3-2. 형식 문법 (0) | 2023.04.10 |
| [Compiler] 3-1. 형식 언어 (0) | 2023.03.23 |